文章标题：Differentially Private Federated Learning/ A Client Level Perspective
文章来源：https://zhuanlan.zhihu.com/p/518310098

作者为哈尔滨工业大学网络安全专业在读博士生Dr.Miao，个人知乎主页为：https://www.zhihu.com/people/Miao

Abstract

联邦学习是隐私保护方面的最新进展。联邦学习中，一个受信任的管理者聚合了由多客户以非中心方式优化的参数。最终收敛得到的联合代表模型被分配到所有客户端，在整个训练过程中无需共享各方数据。然而，这种方案容易受到差分攻击，并且可以从参与联邦优化的任意一方的贡献中进行攻击。在这种攻击下，通过分析分布式模型，泄露了单个客户端在训练过程中的贡献和关于其数据的信息。为应对这个问题，本文提出了一个在联邦优化中对客户端进行差分隐私保护的算法。目的是隐藏单个客户端在训练过程中的贡献，权衡隐私损失和模型表现。实验研究表明，当充分多的客户端参与训练时，本文所提方法能以较小的模型表现损失为代价，以实现客户端级的差分隐私保护。

Introduction

最近，机器学习中的安全问题备受瞩目。这主要归功于大数据与深度学习的结合以及大规模数据挖掘的发展。然而，随着越来越多的机器学习服务成为人们日常生活的一部分，需要采取特殊的措施来保护数据中的隐私。不幸的是，匿名处理常常是不够的，并且标准的机器学习方法在很大程度上忽略了隐私。

在联邦学习中，多个客户端以非中心化的方式共同学习得一个模型。学习任务变成了各个客户端的模型参数被一个受信任的管理者聚合，然后将聚合后的模型同步给各个客户端。

客户不透露他们的数据是在隐私保护方面的进步，但是，当以传统方式学习模型时，其参数会泄露有关训练期间使用的数据的信息。为了解决这个问题，差分隐私（dp）的概念。目的是确保学习的模型不会泄露在训练期间是否使用了某个数据。

本文提出了一个算法，将差分隐私保护机制融入到联邦学习中。然而，与文献[1]不同的是，本文的目的不是仅保护单个数据，而是想确保一个学习模型不会泄露单个客户端是否参与了非中心化训练。这意味着客户端的整个数据集受到保护，免受来自其他客户端的差异攻击。

本文的主要贡献为：首先，展示了当客户端的参与被隐藏时，联邦学习得到的模型依然具有较好的表现。本文证明了以较小的模型表现为代价，本文所提算法可以实现客户端级的差分隐私。一个独立的研究[6]提出了一个相似的客户端级差分隐私的方法。然而，实验设置有所不同，文献[6]还包括元素级隐私措施。第二，本文提出了在非中心化训练过程中动态适应差分隐私的保护机制。实验研究表明这种动态方式可以加强模型表现。这种适应关于最新的具有差分隐私的中心训练方法而言是无益的。可以将这种区别与这样一个事实联系起来，即与集中式学习相比，联邦学习中的梯度在整个训练过程中表现出对噪声和批次大小的不同敏感性。

Background

Federated Learning

在联邦学习中[5]，管理者与客户端之间的通信可能是受限的（例如，手机）并且容易被监听。联邦优化的挑战是以客户端与管理者之间最小的信息交换来学习一个模型。除此之外，客户端数据可能具有非独立同分布性、不平衡性以及大规模分布性。文献[5]提出了“联邦平均”算法来应对这些挑战。在管理者与客户端的多轮通信中，一个中心化模型被训练。在每一轮通信中，管理者将现有模型同步给一部分客户端。客户端执行本地优化。为了降低通信量，客户端可能在一轮通信中，执行多次最小批次梯度下降。接下来，优化后的模型被发送给管理者，由它负责聚合（例如，聚合操作可以是平均）得到一个新的中心模型。根据新的中心模型的性能，训练要么停止，要么开始新的通信轮次。在联邦学习中，客户端不共享数据，只共享模型参数。

Learning with differential privacy

对于在中心化模型学习时保护数据级别的差分隐私已有大量的研究工作，可以通过将差分隐私保护随机化机制（例如，高斯机制）加入到学习过程来达到该目的。

本文对差分隐私随机化机制的定义与文献[1]相同：

一个随机化机制 $M: D \rightarrow R$ ，如果对于任意两个相近输入 $d,d^{‘}\in D$ 和任意的输出子集 $S\subseteq R$ 满足 $P[M(d)\in S]\leq e^{\epsilon}Pr[M(d^{‘})\in S]+\delta$ ，则称域 $D$ 和范围 $R$ 满足 $(\epsilon,\delta)$-DP。在该定义中，$\delta$ 为 $\epsilon$ 差分隐私被攻击的可能性。

高斯机制（GM）近似于一个具有差分隐私机制的实值函数 $f:D\rightarrow R$ 。具体地，高斯机制添加校准的高斯噪声到函数数据集的敏感度 $S_{f}$ 中。该敏感度被定义为两个相近输入 $d^{‘},d$ 的绝对距离 $||f(d)-f(d^{‘})||_{2}$ 。高斯机制被定义为 $M(d)=f(d)+\mathcal{N}(0,\sigma^{2}S_{f}^{2})$ 。

下面的内容中，假设 $\sigma$ 与$\epsilon$ 被固定，并且使用一个查询操作来对高斯机制关于 $f(d)$ 的一个单一的近似进行评估。然后，给出 $\epsilon$ 差分隐私被攻击的概率上界，根据 $\delta\leq \frac{4}{5}{\rm exp}[-(\sigma\epsilon)^{2}/2]$ （文献[4]中的定理3.22）。应该注意到 $\delta$ 随对高斯机制的连续查询次数的增多而增长。因此，为了保护隐私，需要根据 $\delta$ 保持追踪。一旦达到关于 $\delta$ 的一个确定的阈值，高斯机制将不再回答任何新的查询。

最近，文献[1]提出了一种差分隐私随机梯度下降算法（dp-SGD）, dp-SGD与最小批次梯度下降算法类似，但是梯度平均步长通过高斯机制来近似。另外，通过对数据的随机抽样分配最小批次。因为 $\epsilon$ 被固定，一个隐私记录对 $\delta$ 进行持续追踪，一旦达到某个确定的阈值，训练将停止。直观地，这意味着一旦学习模型泄露某个数据是否属于训练集的概率超过了某一阈值，训练将停止。

lient-sided differential privacy in federated optimization

本文提出了将随机化机制加入到联邦学习中。然而，与文献[1]不同，本文的目的不是在模型学习时保护单一数据的贡献。本文的目的是保护客户端的整个数据集。即，确保在非中心化训练中，学习模型将不会泄露一个客户端是否参与了训练，同时保持模型较优的表现。

Method

在联邦优化[5]框架中，在每一轮通信后，中心管理者对客户端模型进行了平均（例如对权重矩阵进行平均）。本文所提算法将使用一个随机化机制改变和近似该平均。这样做的目的是在聚合中隐藏单个客户端的贡献，从而在整个非中心化的学习过程中隐藏。

用于近似平均的随机化机制由两个步骤组成：

1. 随机子采样(Random sub-sampling)：设 $K$ 是客户端总数。在每一轮通信中，随机采样 $m_{t}\leq K$ 个客户端组成随机子集 $Z_{t}$ 。然后，管理者将中心模型 $w_{t}$ 同步给 $Z_{t}$ 中的客户端。各个客户端基于它们自身的数据对中心模型进行优化，则 $Z_{t}$ 中的客户端拥有了互不相同的本地模型 $\{w^{k}\}^{m_{t}}_{k=0}$ 。优化后的本地模型和中心模型之间的差异被称为客户端 $k$ 的更新 $\Delta w^{k}=w^{k}-w_{t}$ 。然后，该更新值被发送给中心管理者。

2. 变形(Distorting)：一个高斯机制被用于变形所有更新的和。这需要了解集合相对于求和运算的敏感度。通过使用真实更新值的缩放版本来加强敏感度：$\Delta\overline{w}^{k}=\Delta w^{k}/\max(1,\frac{||\Delta w^{k}||_{2}}{S})$ 。缩放比例确保了第二项是受限制，即对于 $\forall k$ ，$||\Delta\overline{w}^{k}||_{2}<S$ 。因此，缩放更新相对于求和操作的敏感度以 $S$ 为上限。高斯机制将噪声添加到所有缩放后的更新值之和中。将高斯机制的输出除以 $m_{t}$ 得到所有客户端更新的真实平均值的近似值，与此同时，禁止了关于单个客户端的重要信息的泄露。

通过将此近似值添加到当前中心模型 $w_{t}$ 中得到新的中心模型 $w_{t+1}$。

$w_{t+1}=w_{t}+\frac{1}{m_{t}}\left(\sum_{k=0}^{m_{t}} \Delta w^{k} / \max \left(1, \frac{\left\|\Delta w^{k}\right\|_{2}}{S}\right) + \mathcal{N}\left(0, \sigma^{2} S^{2}\right)\right)$

当将高斯机制乘以 $\frac{1}{m_{t}}$时，注意到平均更新值的变形由噪声方差$\frac{\sigma^{2} S^{2}}{m_{t}}$所控制。然而，这种变形不应该超过一定的限制。否则，更新的平均值的大部分信息被添加的噪声所破坏，并且将不会有任何的学习提升。高斯机制和随机子采样都是随机化机制。（文献[1]在dp-SGD中使用了这种近似平均。然而，其针对梯度平均做了近似，在每一轮迭代中隐藏了单个数据的梯度信息）。因此，当随机化机制提供了一个平均近似时，$\sigma$ 和 $m$ 也决定了隐私损失。

为了追踪隐私损失，本文使用了由Abadi等人[1]提出的方法。这种计算方法提供了关于已有隐私损失更紧的界，相比于标准的组合定理（文献[4]中的3.14）。管理者每次同步新模型时，将会基于给定的 $\epsilon,\sigma,m$ 评估 $\delta$ 。一旦 $\delta$ 达到某个确定的阈值（该阈值可以是某一客户端贡献被泄露的可能性很高时），训练将停止。为了确保许多人的隐私保护不是以泄露有关少数几个信息为代价的，我们必须确保 $\delta\ll \frac{1}{K}$ ，更多细节见文献[4]的2.3节。

选择 $S$：当对贡献值进行裁剪时，存在一个平衡。一方面，$S$ 应该选择较小的值，以便使得噪声方差较小。另一方面，又想尽可能保持原始的贡献值（因此 $S$ 不能太小）。根据文献[1]所提方法，在每一轮通信中，使用原始贡献值的中位数为裁剪界 $S={\rm median}\{\Delta w^{k}\}_{k\in Z_{t}}$ 。我们对中位数不使用随机化机制，这样严格来说侵犯了隐私。然而，中位数泄露信息的可能性很小（未来的工作将包含这样的隐私措施)。

选择 $\sigma$ 和 $m$：当固定 $S$ 后，变形程度和隐私损失受 $r=\frac{\sigma^{2}}{m}$ 控制。隐私损失随着 $\sigma$ 的增加而变大，随着 $m$ 的增大而减小。隐私计算表明，当 $r=\frac{\sigma^{2}}{m}$ 固定时，即对于相同的变形程度，当 $\sigma$ 和 $m$ 均比较小时，隐私损失也较小。当确定了变形程度 $r$ 的上界以及客户端采样数 $m$ 的下界后，就很容易确定 $\sigma$ 的取值。然而，$m$ 的下界很难估计。这是因为，联邦学习场景下，各个客户端数据是非独立同分布的且各自的贡献也不尽相同。因此，本文将客户端更新值的相似性定义为客户端之间的差别 $V_{c}$ 。

定义设 $\Delta w_{i,j}$ 为第 $t$ 通信中梯度矩阵 $\Delta w\in\mathbb{R}^{q\times p}$ 的第 $i$ 行、第 $j$ 列的值。为使得表述清晰，在符号表示中省略通信轮次的标号。

所有 $K$ 个客户端的更新参数的方差为：

$VAR[\Delta w_{i,j}]=\frac{1}{K}\sum\limits_{k=0}^{K}(\Delta w_{i,j}^{k}-\mu_{i,j})^{2}$

其中，$\mu_{i,j}=\frac{1}{K}\sum_{k=1}^{K}\Delta w_{i,j}^{k}$ 。

定义 $V_{c}$ 为更新矩阵中所有参数值的方差的和：

$V_{c}=\frac{1}{q\times p}\sum\limits_{i=0}^{q}\sum\limits_{j=0}^{p}VAR[\Delta w_{i,j}]$

进一步，更新尺度 $U_{s}$ 被定义为：

$U_{s}=\frac{1}{q\times p}\sum\limits_{i=0}^{q}\sum\limits_{j=0}^{p}\mu_{i,j}^{2}$

Experiments

为了测试本文所提算法，本文进行了模拟联邦学习。进行了与文献[5]中相似的实验。本文将排好序的MNIST数据集进行分片。每个客户端拥有两个分片。这种方式使得大多数客户端仅拥有两个数字的手写样本。因此，单个客户端永远无法在其数据上训练模型，使其达到所有十个数字的高分类精度。

实验分别设置 $K\in\{100,1000,10000\}$ ，然后检验联邦学习中的差分隐私。实验中，每个客户端拥有600个样本，对于 $K\in\{1000,10000\}$ 而言，数据样本是重复的。

对于全部三种 $K$，我们对下述参数进行了基于格搜索的交叉验证：

每个客户端的训练数据的批次大小 $B$
每个客户端的本地更新次数 $E$
每轮训练中参与客户端的数量 $m$
高斯机制参数 $\sigma$

根据文献[1]，我们固定 $\epsilon$ 为8。训练过程中，我们追踪隐私损失。一旦 $\delta$ 达到 $e-3,e-5,e-6$ 分别对于100,1000,10000个客户端而言，训练将停止。另外，实验也分析了训练过程中，客户端之间的差异。实验代码的地址为https://github.com/cyrusgeyer/DiffPrivate_FedLearning。

Results

在基于格搜索的交叉验证中，寻找可以达到最高准确率的模型同时关于 $\delta$ 保持在相应界限之下。除此之外，当多个模型达到相同的准确率时，首选通信轮数较小的。

表1列出了对于 $K\in\{100,1000,10000\}$ 找到的最优的模型。表中列出了准确率ACC，通信轮次CR和产生的通信消耗量CC。通信消耗量被定义为在训练过程中模型被客户端发送的次数，$\sum_{t=0}^{T}m_{t}$ 。另外，作为基准，表1也列举了非差分隐私模型达到的最优表现（仅针对 $K=100$ 而言)。

表1：差分隐私联邦学习的实验结果和非差分隐私联邦学习的实验结果的比较。隐私预算为 $\epsilon=8$ ，客户端数量分别为100，1000，10000。$\delta^{‘}$ 是 $\epsilon$ -差分隐私能接受的最高概率。一旦达到 $\delta^{‘}$ ，训练将被停止。准确率为ACC，通信轮次为CR，通信消耗为CC。

在图1展示了训练过程中所有四个性能最佳的模型的准确性。图2为对于 $K=100$ 非差分隐私联邦优化的准确率、客户端之间的差异以及更新尺度在整个训练过程中的变化。

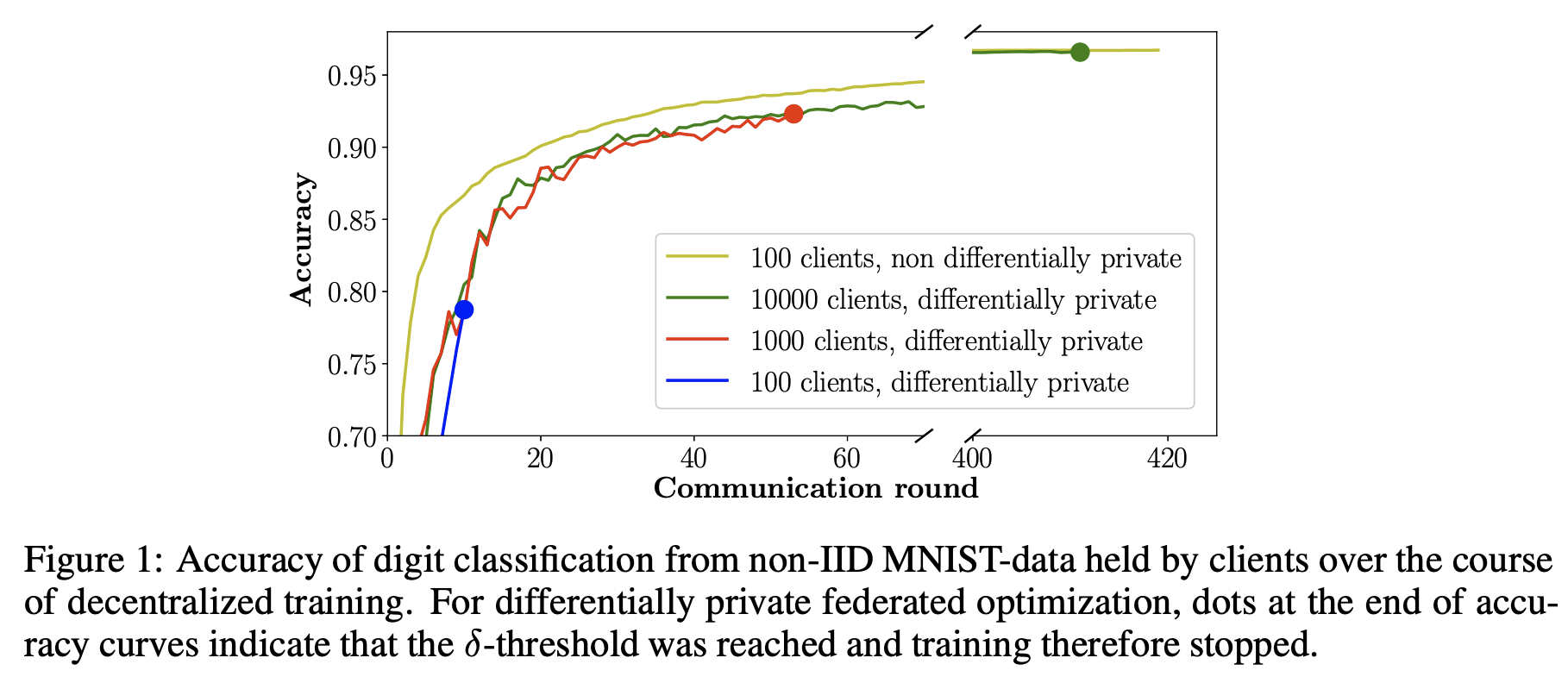
图1：在各个客户端所拥有的数据为非独立同分布的且采用非中心式训练的情况下，手写数字分类的准确率。对于差分隐私联邦优化，每个准确率曲线结尾的点表示了一旦达到阈值 $\delta$ ，训练就停止了。

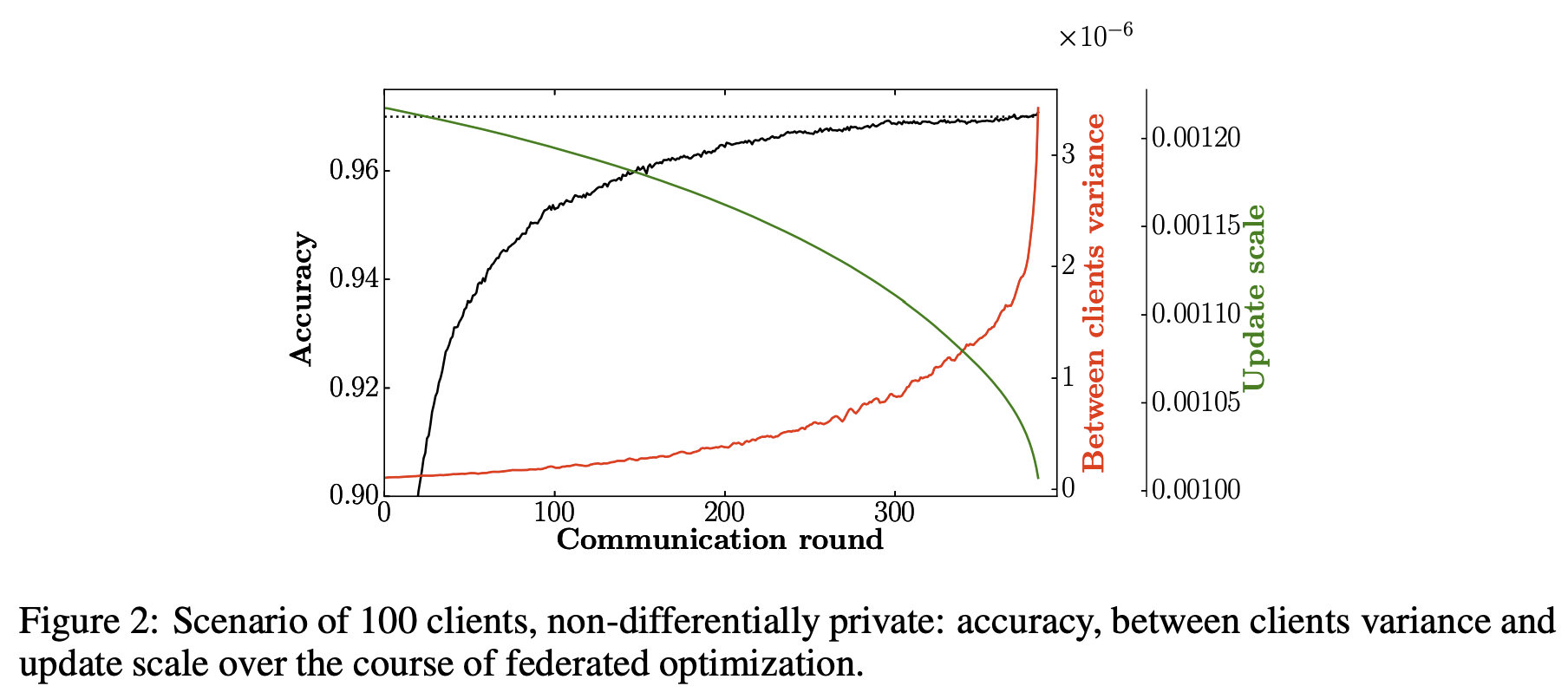
图2：100个客户端，非差分隐私联邦优化过程中，准确率、客户端间的差异以及更新尺度随通信轮次的增加的变化。

Discussion

正如预期，模型表现主要受参与训练的客户端数量的影响。对于100和1000个客户端数量，模型准确率没有达到收敛，同时比非差分隐私联邦学习的表现差。然而，对应于100个客户端和1000个客户端模型78\%和92\%的准确率依然比任何客户端仅使用它们自己的数据训练的模型所达到的准确率高。$K$ 处于这个数量级范围中，差分隐私至关重要，同时联邦训练的模型仍将使任何参与的客户端均获得收益。一个实际的例子是医院。几百家医院共同学习一个模型，同时还隐藏了关任何一家医院的信息。除此之外，共同训练的模型将被用于客户端进一步训练的初始模型。

对于 $K=10000$ ，差分隐私模型几乎达到了与非差分隐私模型一样的准确率。这意味着对于有很多客户端参与的场景，差分隐私联邦学习几乎在模型表现方面没有下降。这些场景包括移动手机和其它用户设备。

在基于格搜索的交叉验证中，我们也发现 $m_{t}$ 的增强模型表现。当观察前期通信轮次时，为了使得 $\sigma_{t}^{2}/m_{t}$ 满足约束，使用小的 $m_{t}$ 和小的 $\sigma^{t}$ 对准确率几乎没有影响。然而，使用小的参数时，隐私损失减小了。这意味着在达到隐私预算前，优化训练的次数将会增加。在之后的通信轮次中，大的 $m_{t}$ 可以使得准确率提升，同时导致了高的隐私消耗，但提升了模型性能。

这个观察结果可以与最近在学习算法信息理论的最新进展联系起来。如图2所示，根据Shwartz-Ziv和Tishby[8]的研究工作，可以将训练分为两个阶段，标签拟合阶段和数据拟合阶段。在标签拟合阶段，各个客户端的更新是相似的，因此 $V_{c}$ 时比较小的。如图2，在开始阶段 $U_{c}$ 是高的，因为对随机初始化的权重执行了重大更新。在数据拟合阶段 $V_{c}$ 增加了。每个客户端的更新值 $\Delta w^{k}$ 不相似，因为每个客户端基于它们的数据集进行优化。然而，$U_{c}$ 大幅收缩，因为模型靠近局部最优，准确率收敛，各客户端的贡献相互抵消。图2展示了 $V_{c}$ 和 $U_{c}$ 的彼此依赖关系。总结：1) 在早期通信阶段，小的客户端集的更新值的平均 $\Delta w_{t}$ 代表了真实的数据分布。2) 在后期阶段，需要平衡（因此更大）客户端比例才能达到更新的一定代表性。3) 高的 $U_{c}$ 使早期更新不易受到噪音的影响。